Compressed Public Keys
ในยุคแรก ๆ ของบิตคอยน์นั้น มีเพียงการสร้าง public key แบบ 65 Bytes เท่านั้น แต่ในเวลาต่อมา เหล่านักพัฒนาในยุคหลังได้พบวิธีการสร้าง public key แบบใหม่ที่มีเพียง 33 Bytes และสามารถทำงานร่วมกันกับโหนดทั้งหมดในขณะนั้นได้ จีงไม่จะเป็นต้องเปลี่ยนแปลงกฎหรือโครงสร้างภายในโปรโตคอลของบิตคอยน์ โดย poublic key แบบใหม่ที่มีขนาด 33 Bytes นี้เรียกว่า compressed public key (public key ที่ถูกบีบอัด) และมีการเรียก public key ที่มีขนาด 65 Bytes ว่า uncompressed public key (public key ที่ไม่ถูกบีบอัด) ซึ่งประโยชน์ของ public key ที่เล็กลงนั้น นอกจากจะช่วยให้การส่ง public key ให้ผู้อื่นทำได้ง่ายขึ้นแล้ว ยังช่วยให้ธุรกรรมมีขนาดเล็กลง และช่วยให้สามารถทำการชำระเงินได้มากขึ้นในบล็อกเดียวกัน
อย่างที่เราได้เรียนรู้จากเนื้อหาในส่วนของ public key เราได้ทราบว่า public key คือจุด (x, y) บนเส้นโค้งวงรี เนื่องจากเส้นโค้งแสดงฟังก์ชันทางคณิตศาสตร์ จุดบนเส้นโค้งจึงเป็นคำตอบของสมการ ดังนั้นหากเรารู้พิกัด x เราก็สามารถคำนวณพิกัด y ได้โดยแก้สมการ y² mod p = (x³ + 7) mod p นั่นหมายความว่าเราสามารถเก็บเพียงพิกัด x ของ public key โดยละพิกัด y ไว้ ซึ่งช่วยลดขนาดของกุญแจและพื้นที่ที่ต้องใช้เก็บข้อมูลลง 256 บิต การลดขนาดลงเกือบ 50% ในทุกธุรกรรมรวมกันแล้วช่วยประหยัดข้อมูลได้มากมายในระยะยาว!
นี่คือ public key ที่ได้ยกเป็นตัวอย่างไว้ก่อนหน้า
```
x = F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A
y = 07CF33DA18BD734C600B96A72BBC4749D5141C90EC8AC328AE52DDFE2E505BDB
```
และนี่คือ public key ที่มีตัวนำหน้า 04 ตามด้วยพิกัด x และ y ในรูปแบบ 04 x y:
```
K = 04F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A07CF33DA18BD734C600B96A72BBC4749D5141C90EC8AC328AE52DDFE2E505BDB
```
uncompressed public key นั้นจะมีตัวนำหน้าเป็น 04 แต่ compressed public key จะมีตัวนำหน้าเป็น 02 หรือ 03 โดยเหตุผลนั้นมาจากสมการ y² mod p = (x³ + 7) mod p เนื่องจากด้านซ้ายของสมการคือ y² คำตอบสำหรับ y จึงเป็นรากที่สอง ซึ่งอาจมีค่าเป็นบวกหรือลบก็ได้ หากมองเชิงภาพ นี่หมายความว่าพิกัด y ที่ได้อาจอยู่เหนือหรือใต้แกน x เราต้องไม่ลืมว่าเส้นโค้งมีความสมมาตร ซึ่งหมายความว่ามันจะสะท้อนเหมือนกระจกโดยแกน x ดังนั้น แม้เราจะละพิกัด y ได้ แต่เราต้องเก็บ เครื่องหมาย ของ y (บวกหรือลบ) หรืออีกนัยหนึ่งคือเราต้องจำว่ามันอยู่เหนือหรือใต้แกน x เพราะแต่ละตำแหน่งแทนจุดที่แตกต่างกันและเป็น public key ที่แตกต่างกัน
เมื่อคำนวณเส้นโค้งวงรีในระบบเลขฐานสองบนสนามจำกัดของเลขจำนวนเฉพาะ p พิกัด y จะเป็นเลขคู่หรือเลขคี่ ซึ่งสอดคล้องกับเครื่องหมายบวก/ลบตามที่อธิบายก่อนหน้านี้ ดังนั้น เพื่อแยกความแตกต่างระหว่างค่าที่เป็นไปได้สองค่าของ y เราจึงเก็บ compressed public key ด้วยตัวนำหน้า 02 ถ้า y เป็นเลขคู่ และ 03 ถ้า y เป็นเลขคี่ ซึ่งช่วยให้ซอฟต์แวร์สามารถอนุมานพิกัด y จากพิกัด x และคลายการบีบอัดของ public key ไปยังพิกัดเต็มของจุดได้อย่างถูกต้อง ดังภาพประกอบต่อไปนี้
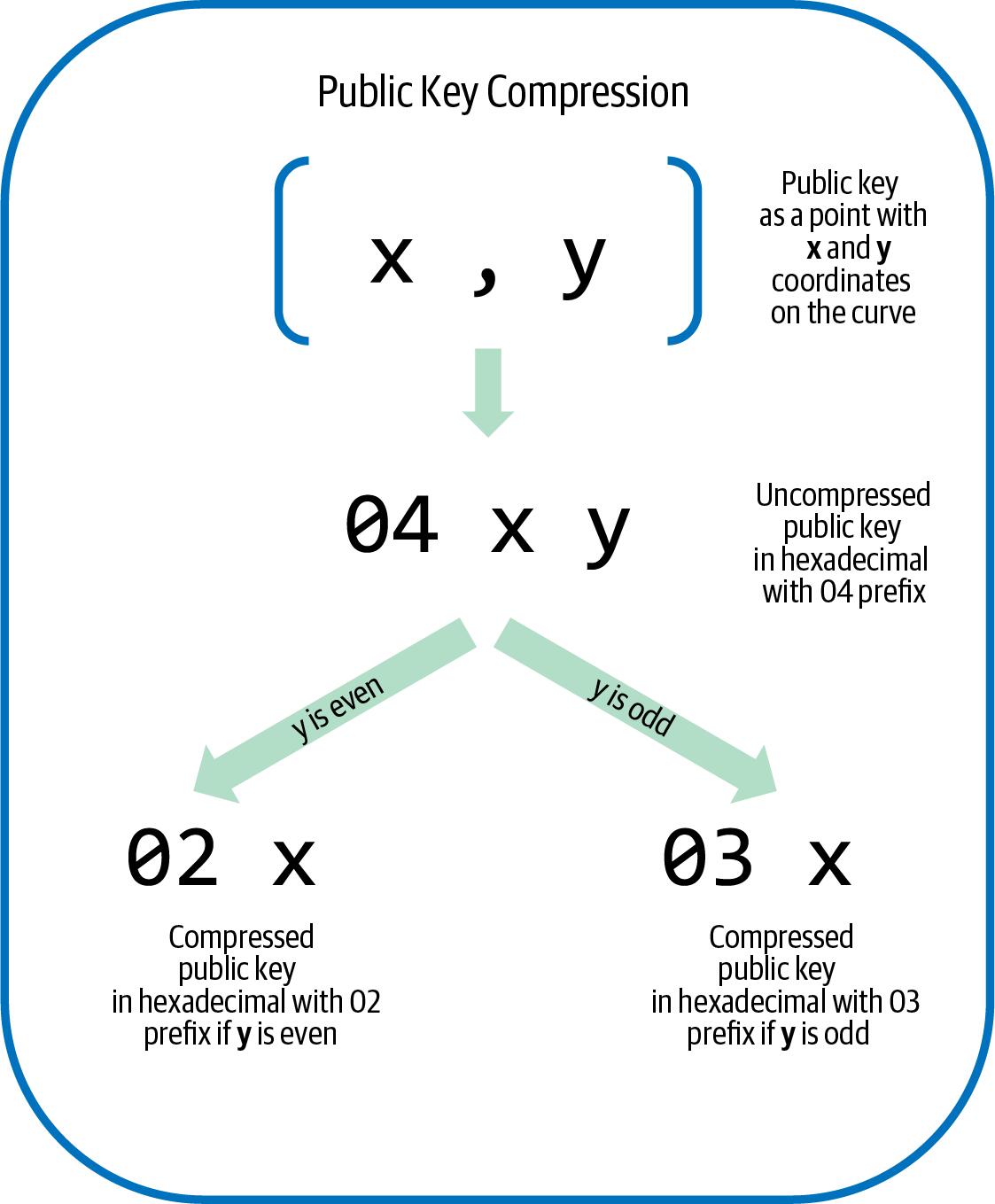 นี่คือ public key เดียวกันกับที่ยกตัวอย่างไว้ข้างต้นซึ่งแสดงให้เห็นในรูป compressed public key ที่เก็บใน 264 บิต (66 ตัวอักษรเลขฐานสิบหก) โดยมีตัวนำหน้า 03 ซึ่งบ่งชี้ว่าพิกัด y เป็นเลขคี่:
```
K = 03F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A
```
compressed public key สอดคล้องกับ private key เดียวกันกับ uncompressed public key หมายความว่ามันถูกสร้างจาก private key เดียวกัน แต่อย่างไรก็ตาม มันก็มีส่วนที่แตกต่างจาก uncompressed public key นั้นคือ หากเราแปลง compressed public key เป็น commitment โดยใช้ฟังก์ชัน HASH160 (RIPEMD160(SHA256(K))) มันจะสร้าง commitment ที่แตกต่างจาก uncompressed public key และจะนำไปสู่ bitcoin address ที่แตกต่างกันในที่สุด สิ่งนี้อาจทำให้สับสนเพราะหมายความว่า private key เดียวสามารถสร้าง public key ในสองรูปแบบที่แตกต่างกัน (แบบบีบอัดและแบบไม่บีบอัด) ซึ่งสร้าง bitcoin address ที่แตกต่างกัน
compressed public key เป็นค่าเริ่มต้นในซอฟต์แวร์บิตคอยน์เกือบทั้งหมดในปัจจุบัน และถูกกำหนดให้ใช้กับคุณสมบัติใหม่บางอย่างที่เพิ่มในการอัปเกรดโปรโตคอลในภายหลัง
อย่างไรก็ตาม ซอฟต์แวร์บางตัวยังคงต้องรองรับ uncompressed public key เช่น แอปพลิเคชันกระเป๋าเงินที่นำเข้า private key จากกระเป๋าเงินเก่า เมื่อกระเป๋าเงินใหม่สแกนบล็อกเชนสำหรับผลลัพธ์และอินพุต P2PKH เก่า มันจำเป็นต้องรู้ว่าควรสแกนกุญแจขนาด 65 ไบต์ (และ commitment ของกุญแจเหล่านั้น) หรือกุญแจขนาด 33 ไบต์ (และ commitment ของกุญแจเหล่านั้น) หากไม่สแกนหาประเภทที่ถูกต้อง อาจทำให้ผู้ใช้ไม่สามารถใช้ยอดคงเหลือทั้งหมดได้ เพื่อแก้ไขปัญหานี้ เมื่อส่งออก private key จากกระเป๋าเงิน WIF ที่ใช้แสดง private key ในกระเป๋าเงินบิตคอยน์รุ่นใหม่จะถูกนำไปใช้แตกต่างกันเล็กน้อยเพื่อบ่งชี้ว่า private key เหล่านี้ถูกใช้ในการสร้าง compressed public key
#siamstr #righttech
อยากแชร์ไปให้คนที่ไม่ได้อยู่บน Nostr อ่านอย่างงั้นเหรอ !?!?!?!? งั้นทางเราขอแนะนำ:
นี่คือ public key เดียวกันกับที่ยกตัวอย่างไว้ข้างต้นซึ่งแสดงให้เห็นในรูป compressed public key ที่เก็บใน 264 บิต (66 ตัวอักษรเลขฐานสิบหก) โดยมีตัวนำหน้า 03 ซึ่งบ่งชี้ว่าพิกัด y เป็นเลขคี่:
```
K = 03F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A
```
compressed public key สอดคล้องกับ private key เดียวกันกับ uncompressed public key หมายความว่ามันถูกสร้างจาก private key เดียวกัน แต่อย่างไรก็ตาม มันก็มีส่วนที่แตกต่างจาก uncompressed public key นั้นคือ หากเราแปลง compressed public key เป็น commitment โดยใช้ฟังก์ชัน HASH160 (RIPEMD160(SHA256(K))) มันจะสร้าง commitment ที่แตกต่างจาก uncompressed public key และจะนำไปสู่ bitcoin address ที่แตกต่างกันในที่สุด สิ่งนี้อาจทำให้สับสนเพราะหมายความว่า private key เดียวสามารถสร้าง public key ในสองรูปแบบที่แตกต่างกัน (แบบบีบอัดและแบบไม่บีบอัด) ซึ่งสร้าง bitcoin address ที่แตกต่างกัน
compressed public key เป็นค่าเริ่มต้นในซอฟต์แวร์บิตคอยน์เกือบทั้งหมดในปัจจุบัน และถูกกำหนดให้ใช้กับคุณสมบัติใหม่บางอย่างที่เพิ่มในการอัปเกรดโปรโตคอลในภายหลัง
อย่างไรก็ตาม ซอฟต์แวร์บางตัวยังคงต้องรองรับ uncompressed public key เช่น แอปพลิเคชันกระเป๋าเงินที่นำเข้า private key จากกระเป๋าเงินเก่า เมื่อกระเป๋าเงินใหม่สแกนบล็อกเชนสำหรับผลลัพธ์และอินพุต P2PKH เก่า มันจำเป็นต้องรู้ว่าควรสแกนกุญแจขนาด 65 ไบต์ (และ commitment ของกุญแจเหล่านั้น) หรือกุญแจขนาด 33 ไบต์ (และ commitment ของกุญแจเหล่านั้น) หากไม่สแกนหาประเภทที่ถูกต้อง อาจทำให้ผู้ใช้ไม่สามารถใช้ยอดคงเหลือทั้งหมดได้ เพื่อแก้ไขปัญหานี้ เมื่อส่งออก private key จากกระเป๋าเงิน WIF ที่ใช้แสดง private key ในกระเป๋าเงินบิตคอยน์รุ่นใหม่จะถูกนำไปใช้แตกต่างกันเล็กน้อยเพื่อบ่งชี้ว่า private key เหล่านี้ถูกใช้ในการสร้าง compressed public key
#siamstr #righttech
อยากแชร์ไปให้คนที่ไม่ได้อยู่บน Nostr อ่านอย่างงั้นเหรอ !?!?!?!? งั้นทางเราขอแนะนำ: 
 นี่คือ public key เดียวกันกับที่ยกตัวอย่างไว้ข้างต้นซึ่งแสดงให้เห็นในรูป compressed public key ที่เก็บใน 264 บิต (66 ตัวอักษรเลขฐานสิบหก) โดยมีตัวนำหน้า 03 ซึ่งบ่งชี้ว่าพิกัด y เป็นเลขคี่:
```
K = 03F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A
```
compressed public key สอดคล้องกับ private key เดียวกันกับ uncompressed public key หมายความว่ามันถูกสร้างจาก private key เดียวกัน แต่อย่างไรก็ตาม มันก็มีส่วนที่แตกต่างจาก uncompressed public key นั้นคือ หากเราแปลง compressed public key เป็น commitment โดยใช้ฟังก์ชัน HASH160 (RIPEMD160(SHA256(K))) มันจะสร้าง commitment ที่แตกต่างจาก uncompressed public key และจะนำไปสู่ bitcoin address ที่แตกต่างกันในที่สุด สิ่งนี้อาจทำให้สับสนเพราะหมายความว่า private key เดียวสามารถสร้าง public key ในสองรูปแบบที่แตกต่างกัน (แบบบีบอัดและแบบไม่บีบอัด) ซึ่งสร้าง bitcoin address ที่แตกต่างกัน
compressed public key เป็นค่าเริ่มต้นในซอฟต์แวร์บิตคอยน์เกือบทั้งหมดในปัจจุบัน และถูกกำหนดให้ใช้กับคุณสมบัติใหม่บางอย่างที่เพิ่มในการอัปเกรดโปรโตคอลในภายหลัง
อย่างไรก็ตาม ซอฟต์แวร์บางตัวยังคงต้องรองรับ uncompressed public key เช่น แอปพลิเคชันกระเป๋าเงินที่นำเข้า private key จากกระเป๋าเงินเก่า เมื่อกระเป๋าเงินใหม่สแกนบล็อกเชนสำหรับผลลัพธ์และอินพุต P2PKH เก่า มันจำเป็นต้องรู้ว่าควรสแกนกุญแจขนาด 65 ไบต์ (และ commitment ของกุญแจเหล่านั้น) หรือกุญแจขนาด 33 ไบต์ (และ commitment ของกุญแจเหล่านั้น) หากไม่สแกนหาประเภทที่ถูกต้อง อาจทำให้ผู้ใช้ไม่สามารถใช้ยอดคงเหลือทั้งหมดได้ เพื่อแก้ไขปัญหานี้ เมื่อส่งออก private key จากกระเป๋าเงิน WIF ที่ใช้แสดง private key ในกระเป๋าเงินบิตคอยน์รุ่นใหม่จะถูกนำไปใช้แตกต่างกันเล็กน้อยเพื่อบ่งชี้ว่า private key เหล่านี้ถูกใช้ในการสร้าง compressed public key
#siamstr #righttech
อยากแชร์ไปให้คนที่ไม่ได้อยู่บน Nostr อ่านอย่างงั้นเหรอ !?!?!?!? งั้นทางเราขอแนะนำ:
นี่คือ public key เดียวกันกับที่ยกตัวอย่างไว้ข้างต้นซึ่งแสดงให้เห็นในรูป compressed public key ที่เก็บใน 264 บิต (66 ตัวอักษรเลขฐานสิบหก) โดยมีตัวนำหน้า 03 ซึ่งบ่งชี้ว่าพิกัด y เป็นเลขคี่:
```
K = 03F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A
```
compressed public key สอดคล้องกับ private key เดียวกันกับ uncompressed public key หมายความว่ามันถูกสร้างจาก private key เดียวกัน แต่อย่างไรก็ตาม มันก็มีส่วนที่แตกต่างจาก uncompressed public key นั้นคือ หากเราแปลง compressed public key เป็น commitment โดยใช้ฟังก์ชัน HASH160 (RIPEMD160(SHA256(K))) มันจะสร้าง commitment ที่แตกต่างจาก uncompressed public key และจะนำไปสู่ bitcoin address ที่แตกต่างกันในที่สุด สิ่งนี้อาจทำให้สับสนเพราะหมายความว่า private key เดียวสามารถสร้าง public key ในสองรูปแบบที่แตกต่างกัน (แบบบีบอัดและแบบไม่บีบอัด) ซึ่งสร้าง bitcoin address ที่แตกต่างกัน
compressed public key เป็นค่าเริ่มต้นในซอฟต์แวร์บิตคอยน์เกือบทั้งหมดในปัจจุบัน และถูกกำหนดให้ใช้กับคุณสมบัติใหม่บางอย่างที่เพิ่มในการอัปเกรดโปรโตคอลในภายหลัง
อย่างไรก็ตาม ซอฟต์แวร์บางตัวยังคงต้องรองรับ uncompressed public key เช่น แอปพลิเคชันกระเป๋าเงินที่นำเข้า private key จากกระเป๋าเงินเก่า เมื่อกระเป๋าเงินใหม่สแกนบล็อกเชนสำหรับผลลัพธ์และอินพุต P2PKH เก่า มันจำเป็นต้องรู้ว่าควรสแกนกุญแจขนาด 65 ไบต์ (และ commitment ของกุญแจเหล่านั้น) หรือกุญแจขนาด 33 ไบต์ (และ commitment ของกุญแจเหล่านั้น) หากไม่สแกนหาประเภทที่ถูกต้อง อาจทำให้ผู้ใช้ไม่สามารถใช้ยอดคงเหลือทั้งหมดได้ เพื่อแก้ไขปัญหานี้ เมื่อส่งออก private key จากกระเป๋าเงิน WIF ที่ใช้แสดง private key ในกระเป๋าเงินบิตคอยน์รุ่นใหม่จะถูกนำไปใช้แตกต่างกันเล็กน้อยเพื่อบ่งชี้ว่า private key เหล่านี้ถูกใช้ในการสร้าง compressed public key
#siamstr #righttech
อยากแชร์ไปให้คนที่ไม่ได้อยู่บน Nostr อ่านอย่างงั้นเหรอ !?!?!?!? งั้นทางเราขอแนะนำ: 
Learning BTC&NOSTR
Learning BTC&NOSTR
สร้างมาเพื่อแชร์เรื่องราวที่ได้ศึกษาจากการเรียนรู...
 ในบิตคอยน์นั้น นอกจากจะใช้ base58check ในการยืนยัน public key แล้ว ก็ยังมีการใช้ในข้อมูลอื่น ๆ ด้วย เพื่อทำให้ข้อมูลนั้นกะทัดรัด อ่านง่าย และตรวจจับข้อผิดพลาดได้ง่ายด้วยรหัสนำหน้า (version prefix) ในการเข้ารหัสแบบ base58check ถูกใช้เพื่อสร้างรูปแบบที่แยกแยะได้ง่าย ซึ่งเมื่อเข้ารหัสด้วย base58 โดยจะมีตัวอักษรเฉพาะที่จุดเริ่มต้นของข้อมูลที่เข้ารหัส base58check ตัวอักษรเหล่านี้ช่วยให้เราระบุประเภทของข้อมูลที่ถูกเข้ารหัสและวิธีการใช้งานได้ง่าย นี่คือสิ่งที่แยกความแตกต่าง ตัวอย่างเช่น ระหว่าง address บิทคอยน์ที่เข้ารหัส base58check ซึ่งขึ้นต้นด้วยเลข 1 กับรูปแบบการนำเข้า private key (WIF - Wallet Import Format) ที่เข้ารหัส base58check ซึ่งขึ้นต้นด้วยเลข 5 ตัวอย่างของ version prefix สามารถดูได้ตามตารางด้านล่างนี้
ในบิตคอยน์นั้น นอกจากจะใช้ base58check ในการยืนยัน public key แล้ว ก็ยังมีการใช้ในข้อมูลอื่น ๆ ด้วย เพื่อทำให้ข้อมูลนั้นกะทัดรัด อ่านง่าย และตรวจจับข้อผิดพลาดได้ง่ายด้วยรหัสนำหน้า (version prefix) ในการเข้ารหัสแบบ base58check ถูกใช้เพื่อสร้างรูปแบบที่แยกแยะได้ง่าย ซึ่งเมื่อเข้ารหัสด้วย base58 โดยจะมีตัวอักษรเฉพาะที่จุดเริ่มต้นของข้อมูลที่เข้ารหัส base58check ตัวอักษรเหล่านี้ช่วยให้เราระบุประเภทของข้อมูลที่ถูกเข้ารหัสและวิธีการใช้งานได้ง่าย นี่คือสิ่งที่แยกความแตกต่าง ตัวอย่างเช่น ระหว่าง address บิทคอยน์ที่เข้ารหัส base58check ซึ่งขึ้นต้นด้วยเลข 1 กับรูปแบบการนำเข้า private key (WIF - Wallet Import Format) ที่เข้ารหัส base58check ซึ่งขึ้นต้นด้วยเลข 5 ตัวอย่างของ version prefix สามารถดูได้ตามตารางด้านล่างนี้
 ภาพต่อไปนี้จะทำให้คุณเห็นภาพของกระบวนการแปลง public key ให้เป็น bitcoin address
ภาพต่อไปนี้จะทำให้คุณเห็นภาพของกระบวนการแปลง public key ให้เป็น bitcoin address
 #siamstr #righttech
อยากแชร์ไปให้คนที่ไม่ได้อยู่บน Nostr อ่านอย่างงั้นเหรอ !?!?!?!? งั้นทางเราขอแนะนำ:
#siamstr #righttech
อยากแชร์ไปให้คนที่ไม่ได้อยู่บน Nostr อ่านอย่างงั้นเหรอ !?!?!?!? งั้นทางเราขอแนะนำ: 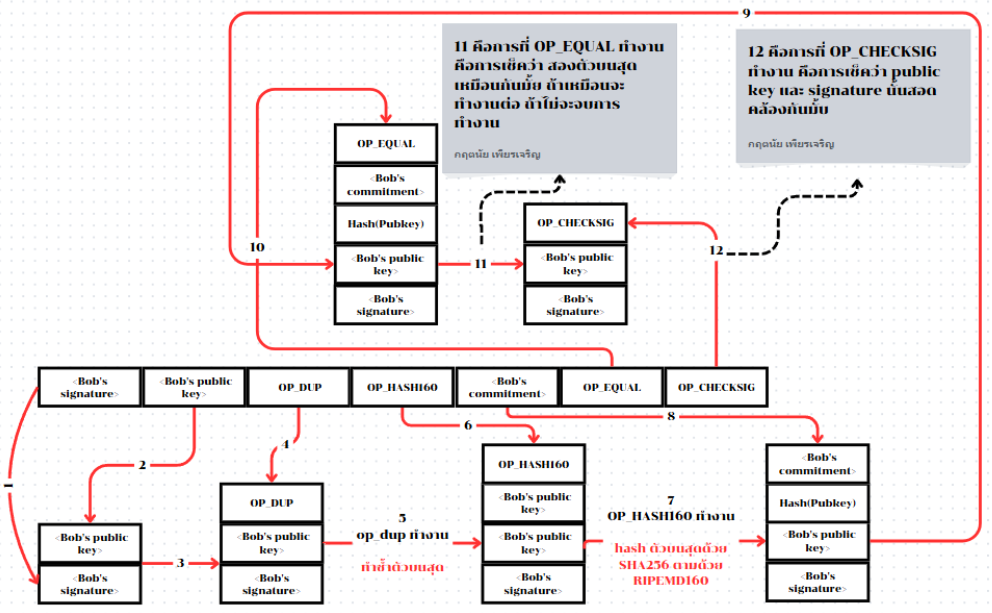 แม้กระบวนการของการ pay-to-publickey-hash(P2PKH) อาจดูซับซ้อน แต่มันทำให้การที่อลิซจ่ายเงินให้บ็อบมีเพียงการยืนยันเพียง 20 ไบต์ต่อ public key ของเขาแทนที่จะเป็นตัวกุญแจเอง ซึ่งจะมีขนาด 65 ไบต์ในเวอร์ชันดั้งเดิมของบิทคอยน์ นั่นเป็นข้อมูลที่น้อยกว่ามากที่บ็อบต้องสื่อสารกับอลิซ
แต่อย่างไรก็ตาม เรายังไม่ได้พูดถึงวิธีที่บ็อบรับ 20 ไบต์เหล่านั้นจากกระเป๋าเงินบิทคอยน์ของเขาไปยังกระเป๋าเงินของอลิซ มีการเข้ารหัสค่าไบต์ที่ใช้กันอย่างแพร่หลาย เช่น เลขฐานสิบหก แต่ข้อผิดพลาดใด ๆ ในการคัดลอกการยืนยันจะทำให้บิทคอยน์ถูกส่งไปยังเอาต์พุตที่ไม่สามารถใช้จ่ายได้ ทำให้พวกมันสูญหายไปตลอดกาล โดยในส่วนถัดไป เราจะดูที่การเข้ารหัสแบบกะทัดรัดและการตรวจสอบความถูกต้อง
#siamstr #righttech
อยากแชร์ไปให้คนที่ไม่ได้อยู่บน Nostr อ่านอย่างงั้นเหรอ !?!?!?!? งั้นทางเราขอแนะนำ:
แม้กระบวนการของการ pay-to-publickey-hash(P2PKH) อาจดูซับซ้อน แต่มันทำให้การที่อลิซจ่ายเงินให้บ็อบมีเพียงการยืนยันเพียง 20 ไบต์ต่อ public key ของเขาแทนที่จะเป็นตัวกุญแจเอง ซึ่งจะมีขนาด 65 ไบต์ในเวอร์ชันดั้งเดิมของบิทคอยน์ นั่นเป็นข้อมูลที่น้อยกว่ามากที่บ็อบต้องสื่อสารกับอลิซ
แต่อย่างไรก็ตาม เรายังไม่ได้พูดถึงวิธีที่บ็อบรับ 20 ไบต์เหล่านั้นจากกระเป๋าเงินบิทคอยน์ของเขาไปยังกระเป๋าเงินของอลิซ มีการเข้ารหัสค่าไบต์ที่ใช้กันอย่างแพร่หลาย เช่น เลขฐานสิบหก แต่ข้อผิดพลาดใด ๆ ในการคัดลอกการยืนยันจะทำให้บิทคอยน์ถูกส่งไปยังเอาต์พุตที่ไม่สามารถใช้จ่ายได้ ทำให้พวกมันสูญหายไปตลอดกาล โดยในส่วนถัดไป เราจะดูที่การเข้ารหัสแบบกะทัดรัดและการตรวจสอบความถูกต้อง
#siamstr #righttech
อยากแชร์ไปให้คนที่ไม่ได้อยู่บน Nostr อ่านอย่างงั้นเหรอ !?!?!?!? งั้นทางเราขอแนะนำ:  บิตคอยน์ใช้เส้นโค้งวงรีเฉพาะและชุดค่าคงที่ทางคณิตศาสตร์ ตามที่กำหนดไว้ในมาตรฐานที่เรียกว่า secp256k1 ซึ่งกำหนดโดยสถาบันมาตรฐานและเทคโนโลยีแห่งชาติ (NIST) เส้นโค้ง secp256k1 ถูกกำหนดโดยฟังก์ชันต่อไปนี้ ซึ่งสร้างเส้นโค้งวงรี: y² = (x³ + 7) บนฟิลด์จำกัด (F_p) หรือ y² mod p = (x³ + 7) mod p
โดยที่ mod p (มอดูโลจำนวนเฉพาะ p) แสดงว่าเส้นโค้งนี้อยู่บนฟิลด์จำกัดของอันดับจำนวนเฉพาะ p ซึ่งเขียนได้เป็น F_p โดย p = 2^256 – 2^32 – 2^9 – 2^8 – 2^7 – 2^6 – 2^4 – 1 ซึ่งเป็นจำนวนเฉพาะที่มีค่ามหาศาล
บิตคอยน์ใช้เส้นโค้งวงรีที่ถูกนิยามบนฟิลด์จำกัดของอันดับจำนวนเฉพาะแทนที่จะอยู่บนจำนวนจริง ทำให้มันมีลักษณะเหมือนรูปแบบของจุดที่กระจัดกระจายในสองมิติ ซึ่งทำให้ยากต่อการจินตนาการภาพ อย่างไรก็ตาม คณิตศาสตร์ที่ใช้นั้นเหมือนกับเส้นโค้งวงรีบนจำนวนจริง
ตัวอย่างเช่น การเข้ารหัสลับด้วยเส้นโค้งวงรี: การแสดงภาพเส้นโค้งวงรีบน F(p) โดยที่ p=17 แสดงเส้นโค้งวงรีเดียวกันบนฟิลด์จำกัดของอันดับจำนวนเฉพาะ 17 ที่มีขนาดเล็กกว่ามาก ซึ่งแสดงรูปแบบของจุดบนตาราง
เส้นโค้งวงรี secp256k1 ที่ใช้ในบิตคอยน์สามารถนึกถึงได้ว่าเป็นรูปแบบของจุดที่ซับซ้อนมากกว่าบนตารางที่มีขนาดใหญ่มหาศาลจนยากจะเข้าใจได้
บิตคอยน์ใช้เส้นโค้งวงรีเฉพาะและชุดค่าคงที่ทางคณิตศาสตร์ ตามที่กำหนดไว้ในมาตรฐานที่เรียกว่า secp256k1 ซึ่งกำหนดโดยสถาบันมาตรฐานและเทคโนโลยีแห่งชาติ (NIST) เส้นโค้ง secp256k1 ถูกกำหนดโดยฟังก์ชันต่อไปนี้ ซึ่งสร้างเส้นโค้งวงรี: y² = (x³ + 7) บนฟิลด์จำกัด (F_p) หรือ y² mod p = (x³ + 7) mod p
โดยที่ mod p (มอดูโลจำนวนเฉพาะ p) แสดงว่าเส้นโค้งนี้อยู่บนฟิลด์จำกัดของอันดับจำนวนเฉพาะ p ซึ่งเขียนได้เป็น F_p โดย p = 2^256 – 2^32 – 2^9 – 2^8 – 2^7 – 2^6 – 2^4 – 1 ซึ่งเป็นจำนวนเฉพาะที่มีค่ามหาศาล
บิตคอยน์ใช้เส้นโค้งวงรีที่ถูกนิยามบนฟิลด์จำกัดของอันดับจำนวนเฉพาะแทนที่จะอยู่บนจำนวนจริง ทำให้มันมีลักษณะเหมือนรูปแบบของจุดที่กระจัดกระจายในสองมิติ ซึ่งทำให้ยากต่อการจินตนาการภาพ อย่างไรก็ตาม คณิตศาสตร์ที่ใช้นั้นเหมือนกับเส้นโค้งวงรีบนจำนวนจริง
ตัวอย่างเช่น การเข้ารหัสลับด้วยเส้นโค้งวงรี: การแสดงภาพเส้นโค้งวงรีบน F(p) โดยที่ p=17 แสดงเส้นโค้งวงรีเดียวกันบนฟิลด์จำกัดของอันดับจำนวนเฉพาะ 17 ที่มีขนาดเล็กกว่ามาก ซึ่งแสดงรูปแบบของจุดบนตาราง
เส้นโค้งวงรี secp256k1 ที่ใช้ในบิตคอยน์สามารถนึกถึงได้ว่าเป็นรูปแบบของจุดที่ซับซ้อนมากกว่าบนตารางที่มีขนาดใหญ่มหาศาลจนยากจะเข้าใจได้
 ตัวอย่างเช่น จุด P ที่มีพิกัด (x, y) ต่อไปนี้เป็นจุดที่อยู่บนเส้นโค้ง secp256k1:
```
P =
(55066263022277343669578718895168534326250603453777594175500187360389116729240,
32670510020758816978083085130507043184471273380659243275938904335757337482424)
```
เราสามารถใช้ Python เพื่อยืนยันว่าจุดนี้อยู่บนเส้นโค้งวงรีได้ตามตัวอย่างนี้:
ตัวอย่างที่ 1: การใช้ Python เพื่อยืนยันว่าจุดนี้อยู่บนเส้นโค้งวงรี
```
Python 3.10.6 (main, Nov 14 2022, 16:10:14) [GCC 11.3.0] on linux
Type "help", "copyright", "credits" or "license" for more information.
> p = 115792089237316195423570985008687907853269984665640564039457584007908834671663
> x = 55066263022277343669578718895168534326250603453777594175500187360389116729240
> y = 32670510020758816978083085130507043184471273380659243275938904335757337482424
> (x ** 3 + 7 - y**2) % p
0
```
ผลลัพธ์เป็น 0 ซึ่งแสดงว่าจุดนี้อยู่บนเส้นโค้งวงรีจริง เพราะเมื่อแทนค่า x และ y ลงในสมการ y² = (x³ + 7) mod p แล้ว ทั้งสองด้านของสมการมีค่าเท่ากัน
ในคณิตศาสตร์ของเส้นโค้งวงรี มีจุดที่เรียกว่า "จุดที่อนันต์" (point at infinity) ซึ่งมีบทบาทคล้ายกับศูนย์ในการบวก บนคอมพิวเตอร์ บางครั้งจุดนี้แทนด้วย x = y = 0 (ซึ่งไม่เป็นไปตามสมการเส้นโค้งวงรี แต่เป็นกรณีพิเศษที่สามารถตรวจสอบได้ง่าย)
มีตัวดำเนินการ + ที่เรียกว่า "การบวก" ซึ่งมีคุณสมบัติคล้ายกับการบวกแบบดั้งเดิมของจำนวนจริงที่เด็กๆ เรียนในโรงเรียน เมื่อมีจุดสองจุด P1 และ P2 บนเส้นโค้งวงรี จะมีจุดที่สาม P3 = P1 + P2 ซึ่งอยู่บนเส้นโค้งวงรีเช่นกัน
ในเชิงเรขาคณิต จุดที่สาม P3 นี้คำนวณได้โดยการลากเส้นระหว่าง P1 และ P2 เส้นนี้จะตัดกับเส้นโค้งวงรีที่จุดเพิ่มเติมอีกหนึ่งจุดพอดี เรียกจุดนี้ว่า P3' = (x, y) จากนั้นให้สะท้อนกับแกน x เพื่อได้ P3 = (x, -y)
มีกรณีพิเศษบางกรณีที่อธิบายความจำเป็นของ "จุดที่อนันต์":
1. ถ้า P1 และ P2 เป็นจุดเดียวกัน เส้น "ระหว่าง" P1 และ P2 ควรขยายเป็นเส้นสัมผัสกับเส้นโค้ง ณ จุด P1 นี้ เส้นสัมผัสนี้จะตัดกับเส้นโค้งที่จุดใหม่อีกหนึ่งจุดพอดี คุณสามารถใช้เทคนิคจากแคลคูลัสเพื่อหาความชันของเส้นสัมผัส เทคนิคเหล่านี้ใช้ได้อย่างน่าแปลกใจ แม้ว่าเราจะจำกัดความสนใจไว้ที่จุดบนเส้นโค้งที่มีพิกัดเป็นจำนวนเต็มเท่านั้น!
2. ในบางกรณี (เช่น ถ้า P1 และ P2 มีค่า x เดียวกันแต่ค่า y ต่างกัน) เส้นสัมผัสจะตั้งฉากพอดี ซึ่งในกรณีนี้ P3 = "จุดที่อนันต์"
3. ถ้า P1 เป็น "จุดที่อนันต์" แล้ว P1 + P2 = P2 ในทำนองเดียวกัน ถ้า P2 เป็นจุดที่อนันต์ แล้ว P1 + P2 = P1 นี่แสดงให้เห็นว่าจุดที่อนันต์มีบทบาทเป็นศูนย์
การบวกนี้มีคุณสมบัติเชิงสมาคม (associative) ซึ่งหมายความว่า (A + B) + C = A + (B + C) นั่นหมายความว่าเราสามารถเขียน A + B + C โดยไม่ต้องมีวงเล็บและไม่มีความกำกวม
เมื่อเรานิยามการบวกแล้ว เราสามารถนิยามการคูณในแบบมาตรฐานที่ต่อยอดจากการบวก สำหรับจุด P บนเส้นโค้งวงรี ถ้า k เป็นจำนวนเต็มบวก แล้ว kP = P + P + P + … + P (k ครั้ง) โปรดทราบว่า k บางครั้งถูกเรียกว่า "เลขชี้กำลัง"
Public Keys
ในระบบคริปโตกราฟีแบบเส้นโค้งวงรี (Elliptic Curve Cryptography) public key ถูกคำนวณจาก private key โดยใช้การคูณเส้นโค้งวงรี ซึ่งเป็นกระบวนการที่ไม่สามารถย้อนกลับได้:
K = k × G
โดยที่:
- k คือ private key
- G คือจุดคงที่ที่เรียกว่า จุดกำเนิด (generator point)
- K คือ public key
การดำเนินการย้อนกลับ ที่เรียกว่า "การหาลอการิทึมแบบไม่ต่อเนื่อง" (finding the discrete logarithm) - คือการคำนวณหา k เมื่อรู้ค่า K - เป็นสิ่งที่ยากมากเทียบเท่ากับการลองค่า k ทุกค่าที่เป็นไปได้ (วิธีการแบบ brute-force)
ความยากของการย้อนกลับนี้คือหลักการความปลอดภัยหลักของระบบ ECC ที่ใช้ในบิตคอยน์ ซึ่งทำให้สามารถเผยแพร่ public key ได้อย่างปลอดภัย โดยที่ไม่ต้องกังวลว่าจะมีใครสามารถคำนวณย้อนกลับเพื่อหา private key ได้
TIP:การคูณเส้นโค้งวงรีเป็นฟังก์ชันประเภทที่นักเข้ารหัสลับเรียกว่า “ trap door function ”:
- เป็นสิ่งที่ทำได้ง่ายในทิศทางหนึ่ง
- แต่เป็นไปไม่ได้ที่จะทำในทิศทางตรงกันข้าม
คนที่มี private key สามารถสร้าง public key ได้อย่างง่ายดาย และสามารถแบ่งปันกับโลกได้โดยรู้ว่าไม่มีใครสามารถย้อนกลับฟังก์ชันและคำนวณ private key จาก public key ได้ กลวิธีทางคณิตศาสตร์นี้กลายเป็นพื้นฐานสำหรับลายเซ็นดิจิทัลที่ปลอมแปลงไม่ได้และมีความปลอดภัย ซึ่งใช้พิสูจน์การควบคุมเงินบิตคอยน์
เริ่มต้นด้วยการใช้ private key ในรูปแบบของตัวเลขสุ่ม เราคูณมันด้วยจุดที่กำหนดไว้ล่วงหน้าบนเส้นโค้งที่เรียกว่า จุดกำเนิด (generator point) เพื่อสร้างจุดอื่นที่อยู่บนเส้นโค้งเดียวกัน ซึ่งคำตอบจะเป็น public key ที่สอดคล้องกัน จุดกำเนิดถูกกำหนดไว้เป็นส่วนหนึ่งของมาตรฐาน secp256k1 และเป็นค่าเดียวกันสำหรับกุญแจทั้งหมดในระบบบิตคอยน์
เนื่องจากจุดกำเนิด G เป็นค่าเดียวกันสำหรับผู้ใช้บิตคอยน์ทุกคน private key (k) ที่คูณกับ G จะได้ public key (K) เดียวกันเสมอ ความสัมพันธ์ระหว่าง k และ K เป็นแบบตายตัวแต่สามารถคำนวณได้ในทิศทางเดียวเท่านั้น คือจาก k ไปยัง K นี่คือเหตุผลที่ public key ของบิตคอยน์ (K) สามารถแบ่งปันกับทุกคนได้โดยไม่เปิดเผย private key (k) ของผู้ใช้
TIP: private key สามารถแปลงเป็น public key ได้ แต่ public key ไม่สามารถแปลงกลับเป็น private key ได้ เพราะคณิตศาสตร์ที่ใช้ทำงานได้เพียงทิศทางเดียวเท่านั้น
เมื่อนำการคูณเส้นโค้งวงรีมาใช้งาน เราจะนำ private key (k) ที่สร้างขึ้นก่อนหน้านี้มาคูณกับจุดกำเนิด G เพื่อหา public key (K):
```
K = 1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDD × G
```
public key (K) จะถูกกำหนดเป็นจุด K = (x, y) โดยที่:
```
x = F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A
y = 07CF33DA18BD734C600B96A72BBC4749D5141C90EC8AC328AE52DDFE2E505BDB
```
เพื่อจะให้เห็นภาพของการคูณจุดด้วยจำนวนเต็มมากขึ้น เราจะใช้เส้นโค้งวงรีที่ง่ายกว่าบนจำนวนจริง (โดยหลักการทางคณิตศาสตร์ยังคงเหมือนกัน) เป้าหมายของเราคือการหาผลคูณ kG ของจุดกำเนิด G ซึ่งเทียบเท่ากับการบวก G เข้ากับตัวเอง k ครั้งติดต่อกัน
ในเส้นโค้งวงรี การบวกจุดเข้ากับตัวเองเทียบเท่ากับการลากเส้นสัมผัสที่จุดนั้นและหาว่าเส้นนั้นตัดกับเส้นโค้งอีกครั้งที่จุดใด จากนั้นจึงสะท้อนจุดนั้นบนแกน x
การเข้ารหัสลับด้วยเส้นโค้งวงรี: การแสดงภาพการคูณจุด G ด้วยจำนวนเต็ม k บนเส้นโค้งวงรี แสดงกระบวนการในการหา G, 2G, 4G เป็นการดำเนินการทางเรขาคณิตบนเส้นโค้งได้ดังนี้
TIP: ในซอฟแวร์ของบิตคอยน์ส่วนใหญ่ใช้ไลบรารีเข้ารหัสลับ libsecp256k1 เพื่อทำการคำนวณทางคณิตศาสตร์เส้นโค้งวงรี
ตัวอย่างเช่น จุด P ที่มีพิกัด (x, y) ต่อไปนี้เป็นจุดที่อยู่บนเส้นโค้ง secp256k1:
```
P =
(55066263022277343669578718895168534326250603453777594175500187360389116729240,
32670510020758816978083085130507043184471273380659243275938904335757337482424)
```
เราสามารถใช้ Python เพื่อยืนยันว่าจุดนี้อยู่บนเส้นโค้งวงรีได้ตามตัวอย่างนี้:
ตัวอย่างที่ 1: การใช้ Python เพื่อยืนยันว่าจุดนี้อยู่บนเส้นโค้งวงรี
```
Python 3.10.6 (main, Nov 14 2022, 16:10:14) [GCC 11.3.0] on linux
Type "help", "copyright", "credits" or "license" for more information.
> p = 115792089237316195423570985008687907853269984665640564039457584007908834671663
> x = 55066263022277343669578718895168534326250603453777594175500187360389116729240
> y = 32670510020758816978083085130507043184471273380659243275938904335757337482424
> (x ** 3 + 7 - y**2) % p
0
```
ผลลัพธ์เป็น 0 ซึ่งแสดงว่าจุดนี้อยู่บนเส้นโค้งวงรีจริง เพราะเมื่อแทนค่า x และ y ลงในสมการ y² = (x³ + 7) mod p แล้ว ทั้งสองด้านของสมการมีค่าเท่ากัน
ในคณิตศาสตร์ของเส้นโค้งวงรี มีจุดที่เรียกว่า "จุดที่อนันต์" (point at infinity) ซึ่งมีบทบาทคล้ายกับศูนย์ในการบวก บนคอมพิวเตอร์ บางครั้งจุดนี้แทนด้วย x = y = 0 (ซึ่งไม่เป็นไปตามสมการเส้นโค้งวงรี แต่เป็นกรณีพิเศษที่สามารถตรวจสอบได้ง่าย)
มีตัวดำเนินการ + ที่เรียกว่า "การบวก" ซึ่งมีคุณสมบัติคล้ายกับการบวกแบบดั้งเดิมของจำนวนจริงที่เด็กๆ เรียนในโรงเรียน เมื่อมีจุดสองจุด P1 และ P2 บนเส้นโค้งวงรี จะมีจุดที่สาม P3 = P1 + P2 ซึ่งอยู่บนเส้นโค้งวงรีเช่นกัน
ในเชิงเรขาคณิต จุดที่สาม P3 นี้คำนวณได้โดยการลากเส้นระหว่าง P1 และ P2 เส้นนี้จะตัดกับเส้นโค้งวงรีที่จุดเพิ่มเติมอีกหนึ่งจุดพอดี เรียกจุดนี้ว่า P3' = (x, y) จากนั้นให้สะท้อนกับแกน x เพื่อได้ P3 = (x, -y)
มีกรณีพิเศษบางกรณีที่อธิบายความจำเป็นของ "จุดที่อนันต์":
1. ถ้า P1 และ P2 เป็นจุดเดียวกัน เส้น "ระหว่าง" P1 และ P2 ควรขยายเป็นเส้นสัมผัสกับเส้นโค้ง ณ จุด P1 นี้ เส้นสัมผัสนี้จะตัดกับเส้นโค้งที่จุดใหม่อีกหนึ่งจุดพอดี คุณสามารถใช้เทคนิคจากแคลคูลัสเพื่อหาความชันของเส้นสัมผัส เทคนิคเหล่านี้ใช้ได้อย่างน่าแปลกใจ แม้ว่าเราจะจำกัดความสนใจไว้ที่จุดบนเส้นโค้งที่มีพิกัดเป็นจำนวนเต็มเท่านั้น!
2. ในบางกรณี (เช่น ถ้า P1 และ P2 มีค่า x เดียวกันแต่ค่า y ต่างกัน) เส้นสัมผัสจะตั้งฉากพอดี ซึ่งในกรณีนี้ P3 = "จุดที่อนันต์"
3. ถ้า P1 เป็น "จุดที่อนันต์" แล้ว P1 + P2 = P2 ในทำนองเดียวกัน ถ้า P2 เป็นจุดที่อนันต์ แล้ว P1 + P2 = P1 นี่แสดงให้เห็นว่าจุดที่อนันต์มีบทบาทเป็นศูนย์
การบวกนี้มีคุณสมบัติเชิงสมาคม (associative) ซึ่งหมายความว่า (A + B) + C = A + (B + C) นั่นหมายความว่าเราสามารถเขียน A + B + C โดยไม่ต้องมีวงเล็บและไม่มีความกำกวม
เมื่อเรานิยามการบวกแล้ว เราสามารถนิยามการคูณในแบบมาตรฐานที่ต่อยอดจากการบวก สำหรับจุด P บนเส้นโค้งวงรี ถ้า k เป็นจำนวนเต็มบวก แล้ว kP = P + P + P + … + P (k ครั้ง) โปรดทราบว่า k บางครั้งถูกเรียกว่า "เลขชี้กำลัง"
Public Keys
ในระบบคริปโตกราฟีแบบเส้นโค้งวงรี (Elliptic Curve Cryptography) public key ถูกคำนวณจาก private key โดยใช้การคูณเส้นโค้งวงรี ซึ่งเป็นกระบวนการที่ไม่สามารถย้อนกลับได้:
K = k × G
โดยที่:
- k คือ private key
- G คือจุดคงที่ที่เรียกว่า จุดกำเนิด (generator point)
- K คือ public key
การดำเนินการย้อนกลับ ที่เรียกว่า "การหาลอการิทึมแบบไม่ต่อเนื่อง" (finding the discrete logarithm) - คือการคำนวณหา k เมื่อรู้ค่า K - เป็นสิ่งที่ยากมากเทียบเท่ากับการลองค่า k ทุกค่าที่เป็นไปได้ (วิธีการแบบ brute-force)
ความยากของการย้อนกลับนี้คือหลักการความปลอดภัยหลักของระบบ ECC ที่ใช้ในบิตคอยน์ ซึ่งทำให้สามารถเผยแพร่ public key ได้อย่างปลอดภัย โดยที่ไม่ต้องกังวลว่าจะมีใครสามารถคำนวณย้อนกลับเพื่อหา private key ได้
TIP:การคูณเส้นโค้งวงรีเป็นฟังก์ชันประเภทที่นักเข้ารหัสลับเรียกว่า “ trap door function ”:
- เป็นสิ่งที่ทำได้ง่ายในทิศทางหนึ่ง
- แต่เป็นไปไม่ได้ที่จะทำในทิศทางตรงกันข้าม
คนที่มี private key สามารถสร้าง public key ได้อย่างง่ายดาย และสามารถแบ่งปันกับโลกได้โดยรู้ว่าไม่มีใครสามารถย้อนกลับฟังก์ชันและคำนวณ private key จาก public key ได้ กลวิธีทางคณิตศาสตร์นี้กลายเป็นพื้นฐานสำหรับลายเซ็นดิจิทัลที่ปลอมแปลงไม่ได้และมีความปลอดภัย ซึ่งใช้พิสูจน์การควบคุมเงินบิตคอยน์
เริ่มต้นด้วยการใช้ private key ในรูปแบบของตัวเลขสุ่ม เราคูณมันด้วยจุดที่กำหนดไว้ล่วงหน้าบนเส้นโค้งที่เรียกว่า จุดกำเนิด (generator point) เพื่อสร้างจุดอื่นที่อยู่บนเส้นโค้งเดียวกัน ซึ่งคำตอบจะเป็น public key ที่สอดคล้องกัน จุดกำเนิดถูกกำหนดไว้เป็นส่วนหนึ่งของมาตรฐาน secp256k1 และเป็นค่าเดียวกันสำหรับกุญแจทั้งหมดในระบบบิตคอยน์
เนื่องจากจุดกำเนิด G เป็นค่าเดียวกันสำหรับผู้ใช้บิตคอยน์ทุกคน private key (k) ที่คูณกับ G จะได้ public key (K) เดียวกันเสมอ ความสัมพันธ์ระหว่าง k และ K เป็นแบบตายตัวแต่สามารถคำนวณได้ในทิศทางเดียวเท่านั้น คือจาก k ไปยัง K นี่คือเหตุผลที่ public key ของบิตคอยน์ (K) สามารถแบ่งปันกับทุกคนได้โดยไม่เปิดเผย private key (k) ของผู้ใช้
TIP: private key สามารถแปลงเป็น public key ได้ แต่ public key ไม่สามารถแปลงกลับเป็น private key ได้ เพราะคณิตศาสตร์ที่ใช้ทำงานได้เพียงทิศทางเดียวเท่านั้น
เมื่อนำการคูณเส้นโค้งวงรีมาใช้งาน เราจะนำ private key (k) ที่สร้างขึ้นก่อนหน้านี้มาคูณกับจุดกำเนิด G เพื่อหา public key (K):
```
K = 1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDD × G
```
public key (K) จะถูกกำหนดเป็นจุด K = (x, y) โดยที่:
```
x = F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A
y = 07CF33DA18BD734C600B96A72BBC4749D5141C90EC8AC328AE52DDFE2E505BDB
```
เพื่อจะให้เห็นภาพของการคูณจุดด้วยจำนวนเต็มมากขึ้น เราจะใช้เส้นโค้งวงรีที่ง่ายกว่าบนจำนวนจริง (โดยหลักการทางคณิตศาสตร์ยังคงเหมือนกัน) เป้าหมายของเราคือการหาผลคูณ kG ของจุดกำเนิด G ซึ่งเทียบเท่ากับการบวก G เข้ากับตัวเอง k ครั้งติดต่อกัน
ในเส้นโค้งวงรี การบวกจุดเข้ากับตัวเองเทียบเท่ากับการลากเส้นสัมผัสที่จุดนั้นและหาว่าเส้นนั้นตัดกับเส้นโค้งอีกครั้งที่จุดใด จากนั้นจึงสะท้อนจุดนั้นบนแกน x
การเข้ารหัสลับด้วยเส้นโค้งวงรี: การแสดงภาพการคูณจุด G ด้วยจำนวนเต็ม k บนเส้นโค้งวงรี แสดงกระบวนการในการหา G, 2G, 4G เป็นการดำเนินการทางเรขาคณิตบนเส้นโค้งได้ดังนี้
TIP: ในซอฟแวร์ของบิตคอยน์ส่วนใหญ่ใช้ไลบรารีเข้ารหัสลับ libsecp256k1 เพื่อทำการคำนวณทางคณิตศาสตร์เส้นโค้งวงรี
 #siamstr #righttech
อยากแชร์ไปให้คนที่ไม่ได้อยู่บน Nostr อ่านอย่างงั้นเหรอ !?!?!?!? งั้นทางเราขอแนะนำ:
#siamstr #righttech
อยากแชร์ไปให้คนที่ไม่ได้อยู่บน Nostr อ่านอย่างงั้นเหรอ !?!?!?!? งั้นทางเราขอแนะนำ: