Nostr: โปรโตคอลทางเลือกใหม่สำหรับโซเชียลมีเดียที่เป็นอิสระ ปลอดภัย และไร้การควบคุม
Nostr คือโปรโตคอลแบบเปิดที่เรียบง่าย ซึ่งช่วยให้สามารถสร้างโซเชียลมีเดียระดับโลกที่กระจายอำนาจและป้องกันการเซ็นเซอร์ได้
จากที่กล่าวข้างต้น เราสามารถพูดได้ว่า Nostr นั้นถูกออกแบบมาให้ใช้งานง่าย โดยมีเป้าหมายหลัก ๆ เพื่อสร้างเครือข่ายโซเชียลระดับโลกที่ปราศจากการเซ็นเซอร์ แล้วทำไมมันถึงทำอย่างนั้นได้? ในจุดนี้เราก็ต้องมาเจาะดูคุณสมบัติหลัก ๆ ของโปรโตคอลที่เรียกว่า Nostr กันก่อน:
เรียบง่าย
- โปรโตคอลนี้ใช้โครงสร้างข้อมูลแบบ Event Object ที่เรียบง่ายและยืดหยุ่น (ซึ่งส่งเป็น JSON ธรรมดา) และใช้การเข้ารหัส แบบ Elliptic-curve มาตรฐานสำหรับคีย์และลายเซ็น
- ช่องทางการสื่อสารที่รองรับเพียงอย่างเดียวคือการเชื่อมต่อ WebSockets จากไคลเอนต์ไปยังรีเลย์
- การออกแบบนี้ทำให้ง่ายต่อการพัฒนาไม่ว่าจะไคลเอนต์หรือรีเลย์ และยังช่วยส่งเสริมความหลากหลายของซอฟต์แวร์
ยืดหยุ่น
- เนื่องจาก Nostr ไม่ได้พึ่งพาเซิร์ฟเวอร์ที่เชื่อถือได้เพียงจำนวนหยิบมือ สำหรับการเคลื่อนย้ายหรือจัดเก็บข้อมูล แต่ใช้เซิร์ฟเวอร์จำนวนมหาศาลและกระจายตัวอยู่ทั่วโลก จึงมีความยืดหยุ่นสูง และมีการกระจายศูนย์อย่างแท้จริง
- โปรโตคอลนี้ถูกออกแบบมาโดยคำนึงถึงความเป็นไปได้ที่รีเลย์จะหายไป และอนุญาตให้ผู้ใช้เชื่อมต่อและเผยแพร่ข้อมูลไปยัง
- รีเลย์จำนวนมากได้ตามต้องการ และยังสามารถเปลี่ยนแปลงได้ตลอดเวลาอีกด้วย
ตรวจสอบได้
- เนื่องจากบัญชี Nostr ใช้การเข้ารหัสแบบ PKE จึงง่ายต่อการตรวจสอบว่าข้อความถูกส่งมาจากผู้ใช้ที่ระบุจริงหรือไม่
เช่นเดียวกับ HTTP หรือ TCP-IP Nostr เป็นโปรโตคอลหรือมาตรฐานแบบเปิดที่ทุกคนสามารถนำไปสร้างต่อยอดได้ มันไม่ใช่แอปหรือบริการที่คุณจำเป็นต้องลงทะเบียน
แล้วทำไมเราถึงต้องการ Nostr?
โซเชียลมีเดียได้พัฒนาเป็นช่องทางสำคัญในการไหลเวียนของข้อมูลทั่วโลก แต่น่าเสียดายที่ระบบโซเชียลมีเดียในปัจจุบันของเรานั้นมีข้อบกพร่องมากมาย:
1. ใช้ความสนใจของคุณเพื่อขายโฆษณา
2. ใช้เทคนิคแปลกๆ เพื่อทำให้คุณเสพติด (อ้างอิงจากข้อ 1)
3. ตัดสินใจว่าจะแสดงเนื้อหาใดให้คุณเห็นโดยใช้อัลกอริทึมลับที่คุณไม่สามารถตรวจสอบหรือเปลี่ยนแปลงได้
4. ควบคุมอย่างเต็มที่ว่าใครสามารถเข้าร่วมและใครถูกเซ็นเซอร์
5. เต็มไปด้วยสแปมและบอท
ด้วยข้อจำกัดเหล่านี้ Nostr จึงเป็นทางเลือกที่น่าสนใจในการสร้างโซเชียลมีเดียที่เป็นอิสระ ปลอดภัย และไร้การควบคุม
#siamstr
อะแฮ่ม ๆ รวมโน๊ตทั้งหมดที่เกี่ยวกับ BTC whitepaper มาแล้ว อ่านทีเดียวยาว ๆ ได้เลย เย้
#siamstr
View Article →
 จากสมมติฐานที่ว่า p > q ความน่าจะเป็นจะลดลงแบบเอกซ์โพเนนเชียล เมื่อจำนวนบล็อกที่ผู้โจมตีต้องไล่ตามทันเพิ่มขึ้น หากเขาไม่สามารถพุ่งขึ้นนำได้อย่างรวดเร็วตั้งแต่แรก โอกาสของเขาก็จะลดลงจนน้อยมาก ๆ เมื่อเขาตามหลังมากขึ้นเรื่อย ๆ
ทีนี้ลองพิจารณาว่า ผู้รับธุรกรรมใหม่ต้องรอเป็นเวลานานเท่าใด จึงจะแน่ใจได้ว่าผู้ส่งไม่สามารถเปลี่ยนแปลงธุรกรรมได้แล้ว เราสมมติว่าผู้ส่งเป็นผู้โจมตี ที่ต้องการให้ผู้รับเชื่อว่าเขาได้รับเงินไปแล้ว จากนั้นจึงเปลี่ยนให้เงินกลับเข้าหาตัวเองหลังจากเวลาผ่านไประยะหนึ่ง ผู้รับจะได้รับแจ้งเมื่อเกิดเหตุการณ์นี้ขึ้น แต่ผู้ส่งหวังว่ามันจะสายเกินไปแล้ว
ผู้รับจะสร้างคู่กุญแจใหม่ และให้กุญแจสาธารณะแก่ผู้ส่งไม่นานก่อนที่จะลงนาม ซึ่งจะป้องกันไม่ให้ผู้ส่งเตรียมบล็อกเชนปลอมไว้ล่วงหน้า โดยการทำงานอย่างต่อเนื่องจนกว่าเขาจะมีโอกาสได้บล็อกที่ยาวพอ จากนั้นจึงดำเนินธุรกรรมในทันที เมื่อส่งธุรกรรมแล้ว ผู้ส่งที่ไม่สุจริตจะเริ่มทำงานอย่างลับ ๆ บนบล็อกเชนคู่ขนาน ที่มีธุรกรรมในเวอร์ชันของเขาเองอยู่
ผู้รับจะรอจนกว่าธุรกรรมจะถูกเพิ่มลงในบล็อก และมีบล็อกที่ถูกเชื่อมต่อตามหลังมาอีก z บล็อก เขาไม่ทราบจำนวนความคืบหน้าที่แน่นอนที่ผู้โจมตีได้ทำไปแล้ว แต่สมมติว่าบล็อกที่สุจริตใช้เวลาเฉลี่ยต่อบล็อกตามที่คาดไว้ ความคืบหน้าที่อาจเกิดขึ้นได้ของผู้โจมตีจะเป็นการแจกแจงแบบปัวซง (Poisson distribution) ซึ่งมีค่าคาดหวังดังนี้:
จากสมมติฐานที่ว่า p > q ความน่าจะเป็นจะลดลงแบบเอกซ์โพเนนเชียล เมื่อจำนวนบล็อกที่ผู้โจมตีต้องไล่ตามทันเพิ่มขึ้น หากเขาไม่สามารถพุ่งขึ้นนำได้อย่างรวดเร็วตั้งแต่แรก โอกาสของเขาก็จะลดลงจนน้อยมาก ๆ เมื่อเขาตามหลังมากขึ้นเรื่อย ๆ
ทีนี้ลองพิจารณาว่า ผู้รับธุรกรรมใหม่ต้องรอเป็นเวลานานเท่าใด จึงจะแน่ใจได้ว่าผู้ส่งไม่สามารถเปลี่ยนแปลงธุรกรรมได้แล้ว เราสมมติว่าผู้ส่งเป็นผู้โจมตี ที่ต้องการให้ผู้รับเชื่อว่าเขาได้รับเงินไปแล้ว จากนั้นจึงเปลี่ยนให้เงินกลับเข้าหาตัวเองหลังจากเวลาผ่านไประยะหนึ่ง ผู้รับจะได้รับแจ้งเมื่อเกิดเหตุการณ์นี้ขึ้น แต่ผู้ส่งหวังว่ามันจะสายเกินไปแล้ว
ผู้รับจะสร้างคู่กุญแจใหม่ และให้กุญแจสาธารณะแก่ผู้ส่งไม่นานก่อนที่จะลงนาม ซึ่งจะป้องกันไม่ให้ผู้ส่งเตรียมบล็อกเชนปลอมไว้ล่วงหน้า โดยการทำงานอย่างต่อเนื่องจนกว่าเขาจะมีโอกาสได้บล็อกที่ยาวพอ จากนั้นจึงดำเนินธุรกรรมในทันที เมื่อส่งธุรกรรมแล้ว ผู้ส่งที่ไม่สุจริตจะเริ่มทำงานอย่างลับ ๆ บนบล็อกเชนคู่ขนาน ที่มีธุรกรรมในเวอร์ชันของเขาเองอยู่
ผู้รับจะรอจนกว่าธุรกรรมจะถูกเพิ่มลงในบล็อก และมีบล็อกที่ถูกเชื่อมต่อตามหลังมาอีก z บล็อก เขาไม่ทราบจำนวนความคืบหน้าที่แน่นอนที่ผู้โจมตีได้ทำไปแล้ว แต่สมมติว่าบล็อกที่สุจริตใช้เวลาเฉลี่ยต่อบล็อกตามที่คาดไว้ ความคืบหน้าที่อาจเกิดขึ้นได้ของผู้โจมตีจะเป็นการแจกแจงแบบปัวซง (Poisson distribution) ซึ่งมีค่าคาดหวังดังนี้:
 เพื่อให้ได้ความน่าจะเป็นที่ผู้โจมตียังคงสามารถไล่ทันได้ เราจะคูณความหนาแน่นของปัวซง สำหรับความคืบหน้าแต่ละระดับที่เขาสามารถทำได้ ด้วยความน่าจะเป็นที่เขาสามารถไล่ทันจากจุดนั้น:
เพื่อให้ได้ความน่าจะเป็นที่ผู้โจมตียังคงสามารถไล่ทันได้ เราจะคูณความหนาแน่นของปัวซง สำหรับความคืบหน้าแต่ละระดับที่เขาสามารถทำได้ ด้วยความน่าจะเป็นที่เขาสามารถไล่ทันจากจุดนั้น:
 จัดเรียงใหม่เพื่อหลีกเลี่ยง infinite tail ของการแจกแจง
จัดเรียงใหม่เพื่อหลีกเลี่ยง infinite tail ของการแจกแจง
 แปลงมันให้เป็น C code
#include <math.h>
double AttackerSuccessProbability(double q, int z)
{
double p = 1.0 - q;
double lambda = z * (q / p);
double sum = 1.0;
int i, k;
for (k = 0; k <= z; k++)
{
double poisson = exp(-lambda);
for (i = 1; i <= k; i++)
poisson *= lambda / i;
sum -= poisson * (1 - pow(q / p, z - k));
}
return sum;
}
เมื่อรันผลลัพธ์บางส่วน เราจะเห็นว่าความน่าจะเป็นลดลงแบบเอกซ์โพเนนเชียลเมื่อ z เพิ่มขึ้น
q=0.1
z=0 P=1.0000000
z=1 P=0.2045873
z=2 P=0.0509779
z=3 P=0.0131722
z=4 P=0.0034552
z=5 P=0.0009137
z=6 P=0.0002428
z=7 P=0.0000647
z=8 P=0.0000173
z=9 P=0.0000046
z=10 P=0.0000012
q=0.3
z=0 P=1.0000000
z=5 P=0.1773523
z=10 P=0.0416605
z=15 P=0.0101008
z=20 P=0.0024804
z=25 P=0.0006132
z=30 P=0.0001522
z=35 P=0.0000379
z=40 P=0.0000095
z=45 P=0.0000024
z=50 P=0.0000006
การแก้หาค่า P ที่น้อยกว่า 0.1%...
P < 0.001
q=0.10 z=5
q=0.15 z=8
q=0.20 z=11
q=0.25 z=15
q=0.30 z=24
q=0.35 z=41
q=0.40 z=89
q=0.45 z=340
#siamstr
แปลงมันให้เป็น C code
#include <math.h>
double AttackerSuccessProbability(double q, int z)
{
double p = 1.0 - q;
double lambda = z * (q / p);
double sum = 1.0;
int i, k;
for (k = 0; k <= z; k++)
{
double poisson = exp(-lambda);
for (i = 1; i <= k; i++)
poisson *= lambda / i;
sum -= poisson * (1 - pow(q / p, z - k));
}
return sum;
}
เมื่อรันผลลัพธ์บางส่วน เราจะเห็นว่าความน่าจะเป็นลดลงแบบเอกซ์โพเนนเชียลเมื่อ z เพิ่มขึ้น
q=0.1
z=0 P=1.0000000
z=1 P=0.2045873
z=2 P=0.0509779
z=3 P=0.0131722
z=4 P=0.0034552
z=5 P=0.0009137
z=6 P=0.0002428
z=7 P=0.0000647
z=8 P=0.0000173
z=9 P=0.0000046
z=10 P=0.0000012
q=0.3
z=0 P=1.0000000
z=5 P=0.1773523
z=10 P=0.0416605
z=15 P=0.0101008
z=20 P=0.0024804
z=25 P=0.0006132
z=30 P=0.0001522
z=35 P=0.0000379
z=40 P=0.0000095
z=45 P=0.0000024
z=50 P=0.0000006
การแก้หาค่า P ที่น้อยกว่า 0.1%...
P < 0.001
q=0.10 z=5
q=0.15 z=8
q=0.20 z=11
q=0.25 z=15
q=0.30 z=24
q=0.35 z=41
q=0.40 z=89
q=0.45 z=340
#siamstr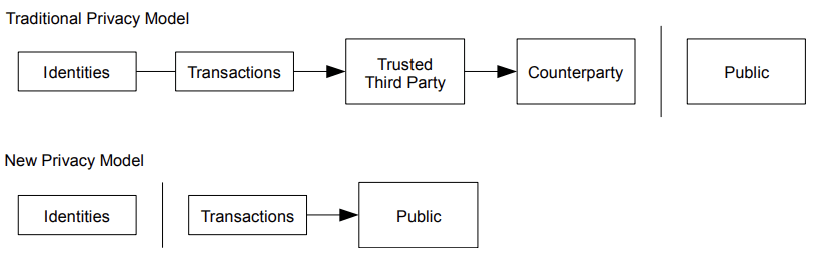 เพื่อเสริมในเรื่องของความปลอดภัย ควรใช้ key pair ใหม่สำหรับการทำธุรกรรมในแต่ละครั้ง เพื่อป้องกันไม่ให้เชื่อมโยงกับเจ้าของคนเดียวกันได้ อย่างไรก็ตาม การเชื่อมโยงบางอย่างยังคงหลีกเลี่ยงไม่ได้ ในธุรกรรมที่มี input หลายรายการ ซึ่งจำเป็นต้องเปิดเผยว่า input เหล่านั้นเป็นของเจ้าของคนเดียวกัน ความเสี่ยงก็คือ หากมีการเปิดเผยตัวตนของเจ้าของคีย์ การเชื่อมโยงอาจเปิดเผยธุรกรรมอื่น ๆ ที่เป็นของเจ้าของรายเดียวกันได้
เพื่อเสริมในเรื่องของความปลอดภัย ควรใช้ key pair ใหม่สำหรับการทำธุรกรรมในแต่ละครั้ง เพื่อป้องกันไม่ให้เชื่อมโยงกับเจ้าของคนเดียวกันได้ อย่างไรก็ตาม การเชื่อมโยงบางอย่างยังคงหลีกเลี่ยงไม่ได้ ในธุรกรรมที่มี input หลายรายการ ซึ่งจำเป็นต้องเปิดเผยว่า input เหล่านั้นเป็นของเจ้าของคนเดียวกัน ความเสี่ยงก็คือ หากมีการเปิดเผยตัวตนของเจ้าของคีย์ การเชื่อมโยงอาจเปิดเผยธุรกรรมอื่น ๆ ที่เป็นของเจ้าของรายเดียวกันได้ ควรสังเกตว่า fan-out (กระจายของธุรกรรม) ซึ่งเป็นกรณีที่ธุรกรรม ธุรกรรมหนึ่งนั้นขึ้นอยู่กับหลายธุรกรรม และธุรกรรมเหล่านั้นเองก็ขึ้นอยู่กับอีกหลายธุรกรรม แต่ไม่ใช่ปัญหาในที่นี้ เพราะไม่มีความจำเป็นในการดึงประวัติการทำธุรกรรมทั้งหมดออกมาเป็นสำเนา
#siamstr
ควรสังเกตว่า fan-out (กระจายของธุรกรรม) ซึ่งเป็นกรณีที่ธุรกรรม ธุรกรรมหนึ่งนั้นขึ้นอยู่กับหลายธุรกรรม และธุรกรรมเหล่านั้นเองก็ขึ้นอยู่กับอีกหลายธุรกรรม แต่ไม่ใช่ปัญหาในที่นี้ เพราะไม่มีความจำเป็นในการดึงประวัติการทำธุรกรรมทั้งหมดออกมาเป็นสำเนา
#siamstr การตรวจสอบดังกล่าวจะเชื่อถือได้ตราบใดที่ node ที่ซื่อสัตย์ยังคงควบคุมเครือข่าย แต่จะมีความเสี่ยงมากขึ้นหากเครือข่ายถูกโจมตีและถูกควบคุม ในขณะที่ node ในเครือข่ายสามารถตรวจสอบธุรกรรมได้ด้วยตัวเอง แต่วิธีการแบบง่ายนี้อาจถูกหลอกลวงโดยการใช้ธุรกรรมปลอมของผู้โจมตี ตราบใดที่ผู้โจมตียังคงสามารถควบคุมเครือข่ายได้ กลยุทธ์หนึ่งในการป้องกันปัญหานี้คือ การรับการแจ้งเตือนจาก node อื่น ๆ ในเครือข่ายเมื่อตรวจพบบล็อกที่ไม่ถูกต้อง ซึ่งจะแจ้งให้ซอฟต์แวร์ของผู้ใช้ดาวน์โหลดบล็อกแบบเต็มและธุรกรรมที่แจ้งเตือน เพื่อยืนยันความไม่สอดคล้องกัน ธุรกิจที่ได้รับการชำระเงินบ่อยครั้งอาจยังคงต้องการรัน node ของตนเอง เพื่อความปลอดภัยที่เป็นอิสระและการตรวจสอบที่รวดเร็วยิ่งขึ้น
#siamstr
การตรวจสอบดังกล่าวจะเชื่อถือได้ตราบใดที่ node ที่ซื่อสัตย์ยังคงควบคุมเครือข่าย แต่จะมีความเสี่ยงมากขึ้นหากเครือข่ายถูกโจมตีและถูกควบคุม ในขณะที่ node ในเครือข่ายสามารถตรวจสอบธุรกรรมได้ด้วยตัวเอง แต่วิธีการแบบง่ายนี้อาจถูกหลอกลวงโดยการใช้ธุรกรรมปลอมของผู้โจมตี ตราบใดที่ผู้โจมตียังคงสามารถควบคุมเครือข่ายได้ กลยุทธ์หนึ่งในการป้องกันปัญหานี้คือ การรับการแจ้งเตือนจาก node อื่น ๆ ในเครือข่ายเมื่อตรวจพบบล็อกที่ไม่ถูกต้อง ซึ่งจะแจ้งให้ซอฟต์แวร์ของผู้ใช้ดาวน์โหลดบล็อกแบบเต็มและธุรกรรมที่แจ้งเตือน เพื่อยืนยันความไม่สอดคล้องกัน ธุรกิจที่ได้รับการชำระเงินบ่อยครั้งอาจยังคงต้องการรัน node ของตนเอง เพื่อความปลอดภัยที่เป็นอิสระและการตรวจสอบที่รวดเร็วยิ่งขึ้น
#siamstr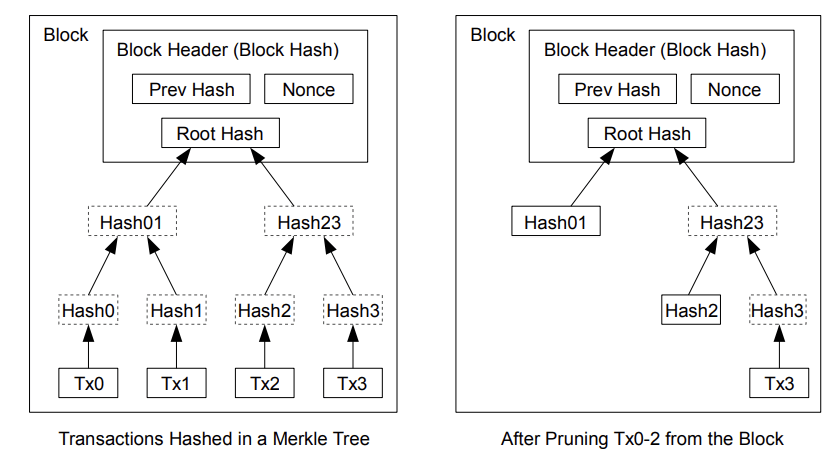 โดยในส่วน header ของบล็อกที่ไม่มีธุรกรรมจะมีขนาดประมาณ 80 ไบต์ หากเราสมมติว่าบล็อกถูกสร้างขึ้นทุก ๆ 10 นาที 80 ไบต์ * 6 * 24 * 365 = 4.2MB ต่อปี โดยที่ระบบคอมพิวเตอร์ทั่วไปที่วางขายในปี 2551 มี RAM 2GB และกฎของมัวร์ทำนายการเติบโตในปัจจุบันที่ 1.2GB ต่อปี การจัดเก็บข้อมูลไม่น่าจะเป็นปัญหาแม้ว่าส่วนหัวของบล็อกจะต้องถูกเก็บไว้ในหน่วยความจำก็ตาม
#siamstr
[2] H. Massias, X.S. Avila, and J.-J. Quisquater, "Design of a secure timestamping service with minimal
trust requirements," In 20th Symposium on Information Theory in the Benelux, May 1999.
[5] S. Haber, W.S. Stornetta, "Secure names for bit-strings," In Proceedings of the 4th ACM Conference
[7] R.C. Merkle, "Protocols for public key cryptosystems," In Proc. 1980 Symposium on Security and
Privacy, IEEE Computer Society, pages 122-133, April 1980.
โดยในส่วน header ของบล็อกที่ไม่มีธุรกรรมจะมีขนาดประมาณ 80 ไบต์ หากเราสมมติว่าบล็อกถูกสร้างขึ้นทุก ๆ 10 นาที 80 ไบต์ * 6 * 24 * 365 = 4.2MB ต่อปี โดยที่ระบบคอมพิวเตอร์ทั่วไปที่วางขายในปี 2551 มี RAM 2GB และกฎของมัวร์ทำนายการเติบโตในปัจจุบันที่ 1.2GB ต่อปี การจัดเก็บข้อมูลไม่น่าจะเป็นปัญหาแม้ว่าส่วนหัวของบล็อกจะต้องถูกเก็บไว้ในหน่วยความจำก็ตาม
#siamstr
[2] H. Massias, X.S. Avila, and J.-J. Quisquater, "Design of a secure timestamping service with minimal
trust requirements," In 20th Symposium on Information Theory in the Benelux, May 1999.
[5] S. Haber, W.S. Stornetta, "Secure names for bit-strings," In Proceedings of the 4th ACM Conference
[7] R.C. Merkle, "Protocols for public key cryptosystems," In Proc. 1980 Symposium on Security and
Privacy, IEEE Computer Society, pages 122-133, April 1980.