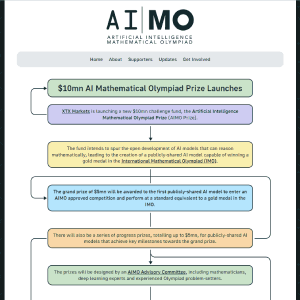
Some loosely organized thoughts on the current Zeitgeist. They were inspired by the response to my recent meta-project mentioned in my previous post

Mathstodon

Terence Tao (@tao@mathstodon.xyz)

I started a crowdsourced meta-project to list all the other crowdsourced mathematical research projects that are currently active and seeking parti...

, where within 24 hours I became aware of a large number of ongoing small-scale collaborative math projects with their own modest but active community (now listed at

MathOverflow

List of crowdsourced math projects actively seeking participants

I believe that with the advent of modern online collaboration platforms (such as Github), proof assistant languages (such as Lean), and (potentiall...

); but they are from the perspective of a human rather than a mathematician. As a crude first approximation, one can think of human society as the interaction between entities at four different scales: 1. Individual humans 2. Small organized groups of humans (e.g., close or extended family; friends; local social or religious organizations; informal sports clubs; small businesses and non-profits; ad hoc collaborations on small projects; small online communities) 3. Large organized groups of humans (e.g., large companies; governments; global institutions; professional sports clubs; large political parties or movements; large social media sites) 4. Large complex systems (e.g., the global economy; the environment; the geopolitical climate; popular culture and "viral" topics; the collective state of science and technology). (1/5)

#SLMath and #ICARM are hosting a joint hybrid workshop on Lean for PDEs, Oct 6-9. Registration is now open:

SLMath

Independent non-profit mathematical sciences research institute founded in 1982 in Berkeley, CA, home of collaborative research programs and public...

Any complex project tends to have both explicitly stated and implicitly unstated target goals. For instance, a Lean formalization project may have as its explicit goal the task of obtaining a formal proof of some mathematical claim X; but there are often unstated goals, such as also formalizing key subclaims and definitions X_1, X_2, ... to X in a fashion that would be suitable for upstreaming to the Mathlib library; learning how to use various collaboration tools and distribute tasks; organically discovering insights to the finer structure of the proof of X that might not be emphasized in previous informal proofs; giving real-world training and experience to novice formalizers; and more generally building a community of humans expert in the art of formalization. In the past, it has generally not been necessary to state these implicit goals because of a strong empirical correlation between the achievement of these goals and the achievement of the explicit goals. In the example of the formalization project, pretty much any human-centric effort to accomplish the explicit goal will end up naturally also achieving most of the implicit goals stated above. So the explicit goal effectively becomes a viable proxy for the broader range of actual goals. (1/2)

Earlier this year, the second #AIMO (artificial intelligence mathematical olympiad) concluded, with the winning team solving 34/50 in the final set of math problems (that had been selected to be harder for AI than the first AIMO). The competition was restricted to open source models and run with a limited amoutn of compute. The AIMO has now conducted a retest of these problems both for the top two teams from that competition (NemoSkills and imagination research), as well as OpenAI's o3 model, both with comparable levels of compute resources, and with high resources. Unsurprisingly, the high resource models did better, with the high resource o3 model scoring as high as 47/50, or even 50/50 if given two tries at each question. On the other hand, the gap between the open source models and the commercial models for a fixed amount of compute was relatively slight. More details of this experiment are available at

AIMO Prize

The gap between commercial and open-source LLMs for Olympiad-level math is shrinking | AIMO Prize

Thomas Bloom and I are launching a crowdsourced project to link up Thomas's erdosproblems.com site with the #OEIS, by systematically calculating the various integer sequences associated with the Erdos problems and crosschecking them against the OEIS database:

What's new

A crowdsourced project to link up erdosproblems.com to the OEIS

Thomas Bloom’s erdosproblems.com site hosts nearly a thousand questions that originated, or were communicated by, Paul Erdős, as well as the...

GitHub

GitHub - teorth/erdosproblems: A community database for the problems on the erdosproblems.com site

A community database for the problems on the erdosproblems.com site - teorth/erdosproblems

The Simons-Laufer Mathematical Sciences institute, or #SLMath (formerly the Mathematical Sciences Research Institute, or MSRI) has recently restructured its program formats, and is now announcing three new research initiatives, whose applications open on Sep 1 2025: * AxIOM (Accelerating Innovation in Mathematics) is a new, month-long research program at SLMath, designed to accelerate innovation and introduce transformative ideas into the mathematical sciences. Programs begin in Spring 2027. * PROOF (Promoting Research Opportunities and Open Forums) is a two-week summer program designed to provide research opportunities for U.S.-based mathematicians, statisticians, and their collaborators in the U.S. and abroad, whose ongoing research may have been impacted by factors such as heavy teaching loads, professional isolation, limited access to funding, heavy administrative duties, personal obligations, or other constraints. Programs begin June-July 2026. * Lasting Alliance Through Team Immersion and Collaborative Exploration (LATTICE) is a yearlong program which provides opportunities for U.S. mathematicians to conduct collaborative research on topics at the forefront of the mathematical and statistical sciences. Programs begin June-July 2026.

SLMath

Independent non-profit mathematical sciences research institute founded in 1982 in Berkeley, CA, home of collaborative research programs and public...

(Disclosure: I am vice-chair of the board of trustees at SLMath.)